回り道よりショートカットする方が近道なのか？！～ピタゴラスの定理から証明する～

こん〇〇は！
今日はいつもぼんやり考えていた、回り道よりショートカットすることで目的地に早く行ける理由と、裏道を頑張って走ってもあまり近道にならない理由を考えてみたいと思います。

今回、『需要絶対ないよなぁ…』というネタをかなり頑張って書いてしまったので、心優しい方は流しながらでも最後までたどり着いてくださるとうれしいです。

[目次]

ピタゴラスの定理
正方形の対角線をジグザグに行くとどうなるのか？
【余談】江戸の数学

ピタゴラスの定理

こんな道を思い浮かべて下さい。

f:id:Slender-G:20190822011459j:plain
地点aから地点bにいくには上に向かっても左に向かっても、2kmの道のりを歩かねばなりません。

これが、もし真ん中をショートカットできるとどうなるでしょう？

f:id:Slender-G:20190822022509j:plain

地点aから地点bに一直線に進むと

$\sqrt{1^2+1^2}≒1.414...$

という事で、明らかに近くなるんですよ。
これを「ピタゴラスの定理」と言って、恐らく子供のころ習ったのをぼんやり思い出してくださった方もいるのではないかと思います。

なんか胡散臭いって言われちゃいそうなので証明してみます。

f:id:Slender-G:20190822011821j:plain

大きい方の正方形(青四角)の面積Sを求めます。

・一辺が(a+b)なので $S=(a+b)^2$

・面積Sは一辺がcの正方形(赤四角)と直角三角形4つの和なので
　 $S=c^2+4×\frac{1}{2}ab=c^2+2ab$ とも表せます
　 $(a+b)^2=c^2+2ab$

∴ $a^2+b^2=c^2$

ということで、直角三角形においては、一番長い辺の2乗はほかの短い辺の2乗の和であることが証明できてしまいました。
この「ピタゴラスの定理」は昔から大好きな方が多くて、証明方法はなんと100種類以上あるそうです。ひやぁ…
Wikipediaには沢山証明の仕方が記載されているので、興味ある方はそちらをどうぞ。(^^)/

正方形の対角線をジグザグに行くとどうなるのか？

なんでこんなことしてるかというと...ふと気になってる事があったのです。

『ショートカットの際、こんな風に小さくジグザグしたらどうなるのか？？』
って気になりませんか？？

f:id:Slender-G:20190822014532j:plain f:id:Slender-G:20190822014558j:plain

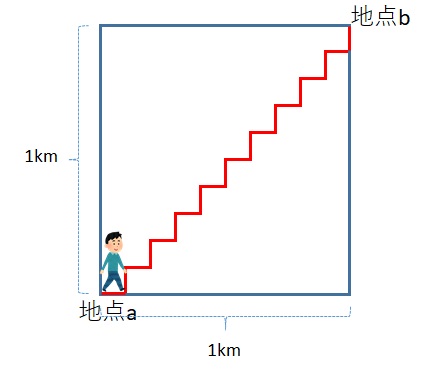
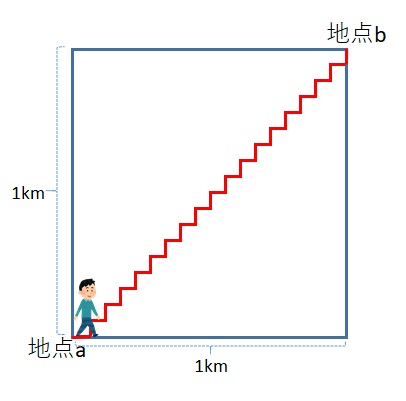
ジグザグする回数をnとした時、 $n=10$ の時の道のりは2km。
$n=20$ でも、 $n=10000$ でも変わりません。小さなジグザグでショートカットしても $\sqrt{2}$ kmにはならず2kmなのです。

しかし、 $n=∞$ とすると対角線は $\sqrt{2}$ になるという。。。

不思議じゃありませんか？
当たり前って思う方もいらっしゃると思いますが、自分はこれがパラドックスにしか思えなくて...「ピタゴラスの定理」で証明できても納得できないもんは出来ないのです...(￣▽￣;)＞

きっと同じこと思った先人の方は山ほどいるだろうとGoogle先生に聞いてみました。

しかし...ピタゴラスの定理はあまりにも鉄板すぎて、私と同じような疑問を持って語ってる人が意外と少なく調べるのに大苦戦。

結果...行き着いた先は「 $\sqrt{2}$ の無理数性」と「無限の曲線」でした。
「無限の曲線」を使って対角線の証明するのは微積必須なのと分かりやすく解説できる気がしないので、今回は何故正方形の対角線が $\sqrt{2}$ の様な無理数になってしまうのか？をスレンダーなりに説明してみたいと思います(出来るんか💦)。

下図のように1辺が1の正方形を考え、その対角線を $x$ とします。

f:id:Slender-G:20190822021856j:plain

ピタゴラスの定理を用いると、
$x^2=1^2+1^2=2$
※この時点で $x=\sqrt{2}$ になっちゃうのですが一旦置いておきます。

AからDへの移動を縦横にものすごく小さな数 $\frac{1}{n}$ (nは自然数)ずつ移動するとします。(ジグザグにね)
AからDにたどり着くのにm回ジグザグするとなると、対角線 $x$ は
$x=\frac{1}{n}×m=\frac{m}{n}$ になる…と思います。

$\frac{m}{n}$ をこれ以上に約分できない数に変換するとします。
例えば、1を100で割る→ $n=100$
その回数 $m=200$
$\frac{m}{n}=\frac{200}{100}$ なので約分出来ちゃいます。

約分すると $\frac{2}{1}$ なので、約分後のそれぞれの数値を $2=b$ 、 $1=a$ とすると
$\frac{m}{n}$ → $\frac{b}{a}$ とすることが出来ます。
※この状態だとbもaも1が公約数になります。

つまり　 $x=\frac{m}{n}=\frac{b}{a}$ 　※すでに胡散臭いですが(笑)

これを　 $x^2=1^2+1^2=2$ 　に代入する

$(\frac{b}{a})^2=2$
∴ $b^2=2a^2$ という式になります。

bは奇数か偶数か？奇数の2乗は奇数でございます。
$b^2=2a^2$ より $b^2$ は何らかの数 $a^2$ に2をかけた数なのでbは偶数であることが証明できます。

bが偶数ということで、整数pを用いて $b=2p$ とすることが出来ます。

そこで、この式を思い出してください。
$(\frac{b}{a})^2=2$

ココに $b=2p$ を代入すると

$(\frac{2p}{a})^2=2$
$\frac{4p^2}{a^2}=2$
∴ $2p^2=a$

あれれ？？
aも偶数になっちゃった…(; ･`д･´)
aが偶数になっちゃうと何がまずいかというと…先ほど前提にした

$\frac{m}{n}$ をこれ以上に約分できない数に変換するとします。
例えば、1を100で割る→ $n=100$
その回数 $m=200$
$\frac{m}{n}=\frac{200}{100}$ なので約分出来ちゃいます。
約分すると2/1なので、約分後のそれぞれの数値を $2=b$ 、 $1=a$ とすると
$\frac{m}{n}$ を約分し $\frac{b}{a}$ とすることが出来ます。
※この状態だとbもaも1が公約数になります。

自分で設定したこれが覆っちゃうのです。
※頭がこんがらがってきた方、申し訳ありませんm(__)m。あとちょっとです。

これは、最初に書いた

AからDへの移動を縦横にものすごく小さな数 $\frac{1}{n}$ (nは自然数)ずつ移動するとします。(ジグザグにね)
AからDにたどり着くのにm回ジグザグするとなると、対角線 $x$ は
$x=\frac{1}{n}×m=\frac{m}{n}$ 　なる…と思います。

これは $x$ を $n$ では割り切れないことを示しているし、1で通分・約分が成り立ってないことを表しています。
∴ $x$ は $\frac{1}{n}$ ずつm回ジグザグに行っても成り立たない
※実際、 $m=200$ 、 $n=100$ の場合、 $x=\frac{m}{n}=2$ になってしまうので $x=\sqrt{2}$ と矛盾します